3  Galería de gráficos

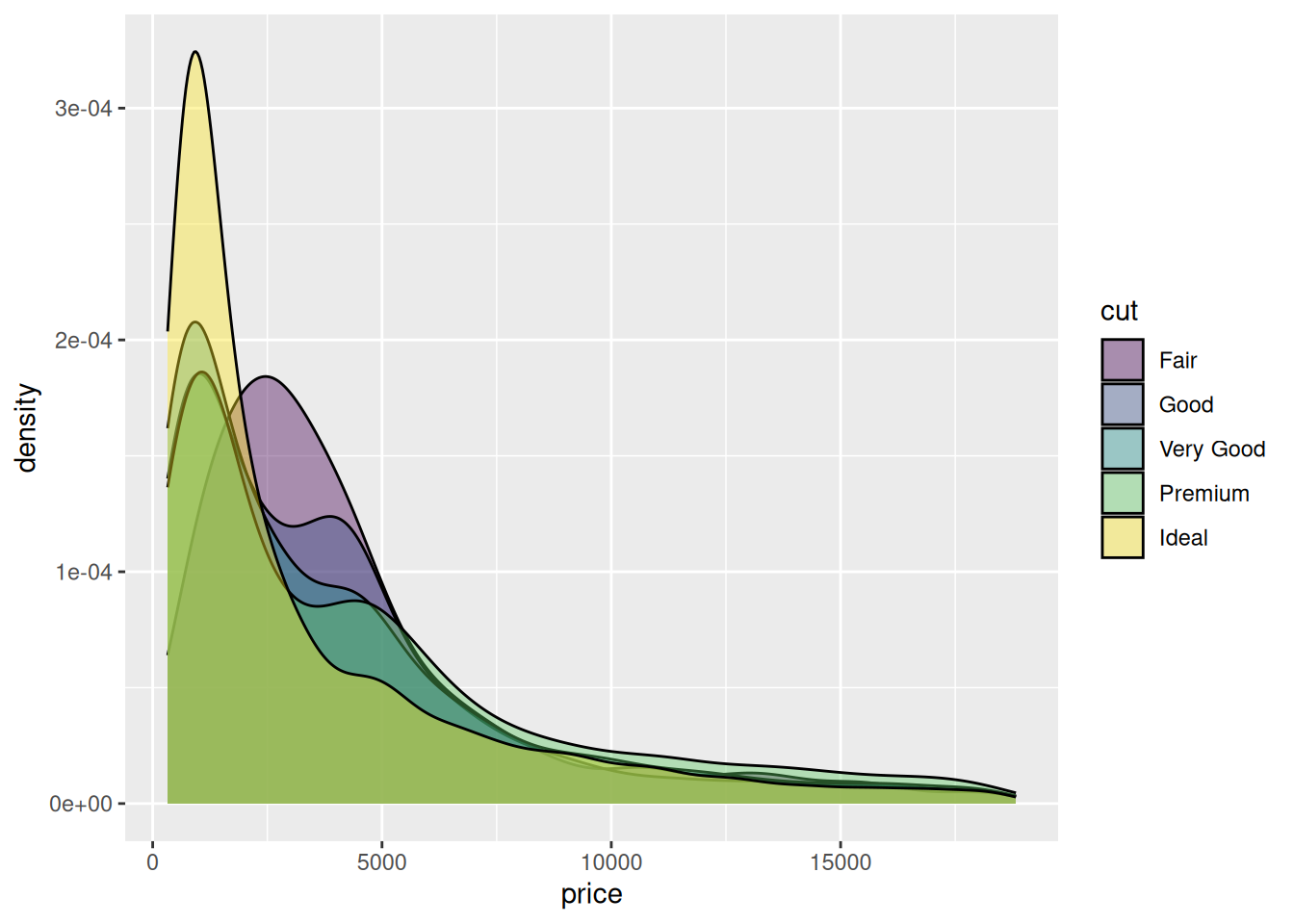
En este capítulo, presentamos los principales tipos de gráficos para visualización de datos que se suelen encontrar en proyectos de análisis de datos. Es esencial saber con qué opciones contamos para después elegir el tipo de gráfico y su modalidad que mejor se adapte a nuestros objetivos.

3.1 Taxonomía de gráficos

A continuación, presentamos una taxonomía tentativa para clasificar diferentes tipos de gráficos en función del tipo de datos y atributos que queremos representar (Wilke, 2019).

3.1.1 Análisis exploratorio de datos

El primer conjunto de tipos de gráficos corresponden a herramientas que podemos utilizar para representar distribuciones de valores. Estos gráficos se suelen emplear para resumir propiedades de conjuntos de datos en la fase de análisis exploratorio.

La Figura 3.1 muestra un primer conjunto de gráficos para este propósito, que representa distribuciones de valores univariantes.

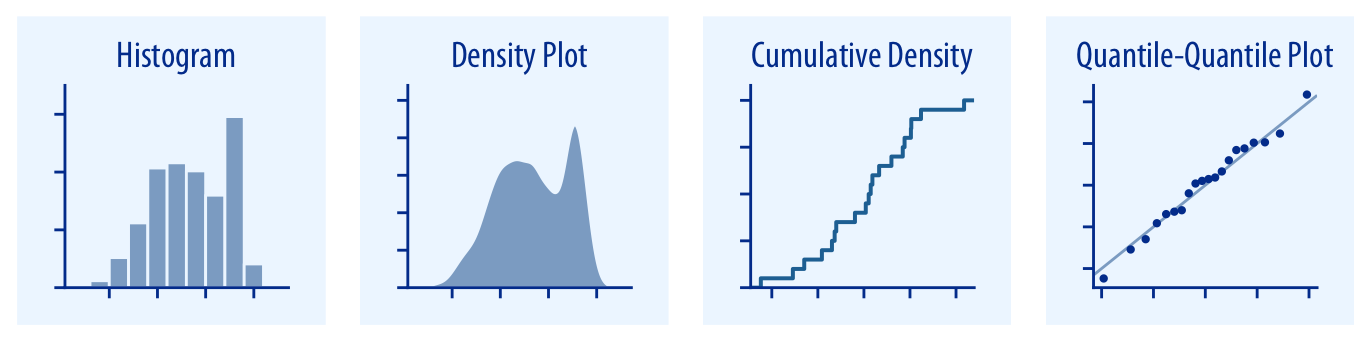
Figura 3.1: Algunos gráficos para representar distribuciones univariantes de valores numéricos. Fuente: (Wilke, 2019).

  • Histograma: El histograma nos permite representar mediante un diagrama de barras verticales el número de ocurrencias o la frecuencia de aparición respecto al total de un intervalo de valores de un atributo numérico. Lo más usual es que los intervalos se representen en el eje horizontal y tengan todos la misma longitud, pero esto no siempre se cumple. Existen diferentes algoritmos y criterios para determinar el número de intervalos generados y el ancho de los mismos.

  • Diagrama de densidad de probabilidad (KDE): Se puede ver como una aproximación continua del histograma, que muestra la frecuencia de aparición de los diferentes valores numéricos de la distribución descrita, es decir, la su función de densidad de probabilidad (o f.d.p.). Para su estimación se emplea el Estimador de Densidad del Kernel (KDE por sus siglas en inglés). Nuevamente, existen diferentes algoritmos y métodos para calcular dicho estimador. Este tipo de función tiene la ventaja de que permite comparar en el mismo gráfico varias f.d.p. simultáneamente, si no rellenamos el área bajo las curvas.

  • Diagrama de densidad acumulada (CDF): Otra visión alternativa sobre cómo está repartida la distribución de valores de un atributo numérico. En este caso se representa la funcisió de densidad de probabilidad acumulada (o CDF, por sus siglas en inglés). Suele ser una herramienta muy versátil, tanto para interpretar mejor una distribución como para identificar qué posible función de distribución de probabilidad teórica se podría ajustar a un conjunto de valores.

  • Gráfico cuantil-cuantil (qqplot): Herramienta gráfica comumnmente empleada para comprobar la bondad del ajuste de una distribución de valores empírica respecto de una distribución teórica. Por ejemplo, un uso frecuente es el de contrastar si los residuos de un modelo de regresión se ajustan de forma creíble a una distribución Normal.

El segundo conjunto de gráficos que muestra la Figura 3.2 recoge herramientas para representar distribuciones de valores de un atributo en función de los valores de otro atributo categórico (factor en R).

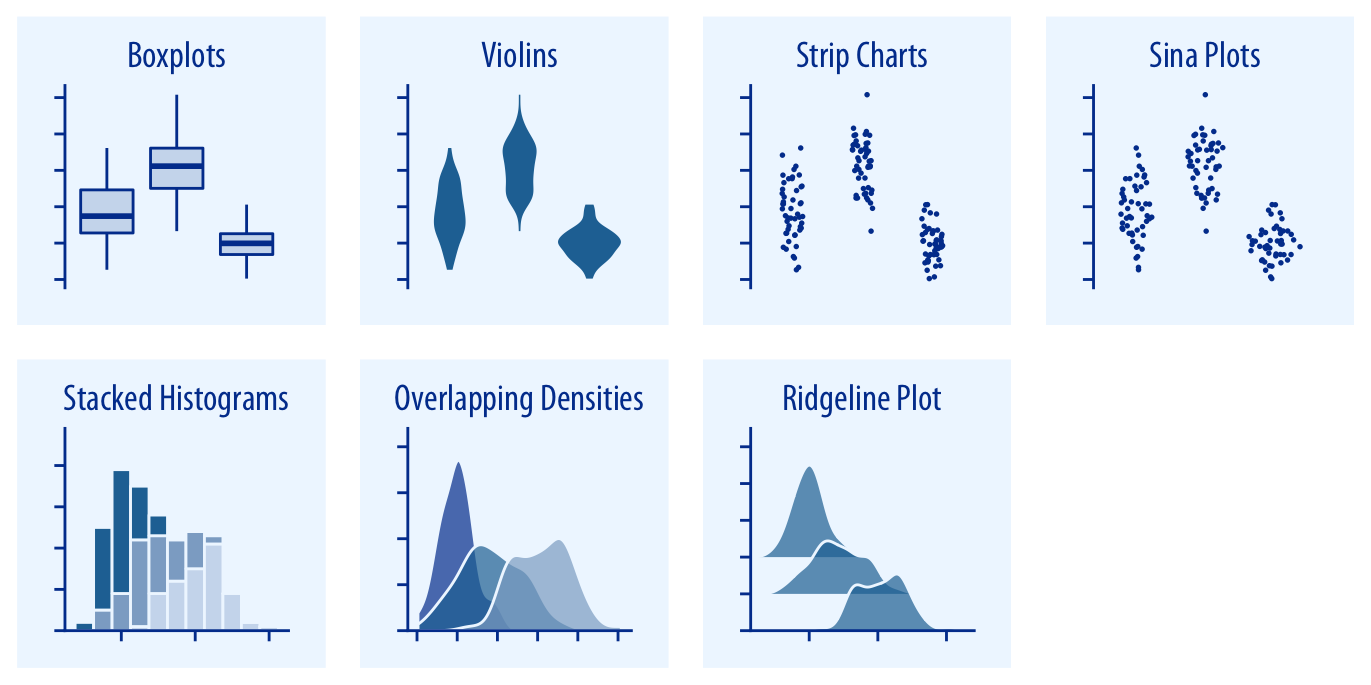
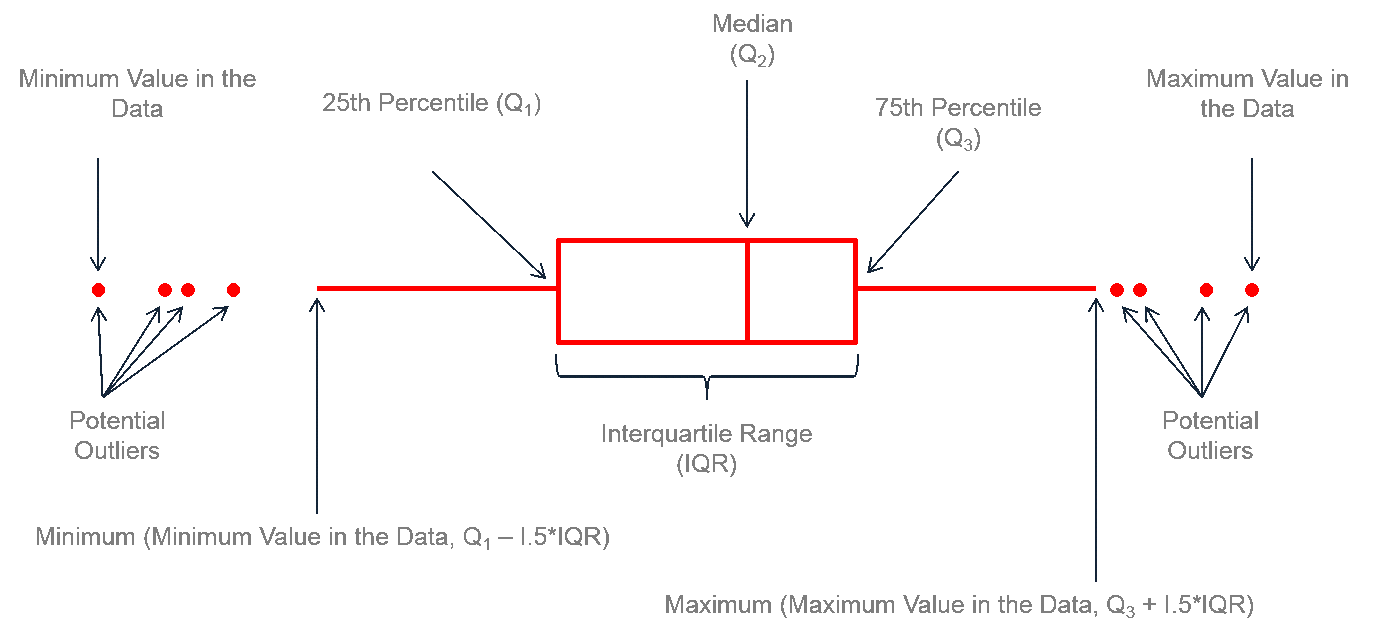
Figura 3.2: Algunos gráficos para representar distribuciones de valores en función de otro atributo categórico. Fuente: (Wilke, 2019).

  • Boxplot: Su creación se debe al insigne estadístico John W. Tukey (Tukey, 1977), que lo propuso como herramienta básica para el EDA. Originalmente también se denominó box-and-whiskers plot, ya que consiste en la combinación de una caja con líneas o “bigotes” a ambos lados. Se trata de un gráfico que muestra un resumen simplificado de la distribución de valores de un atributo numérico, centrándose en cinco estadísticos de resumen claves que se muestran en la Figura 3.3:

    • Mediana: se representa mediante una línea dentro de la caja.
    • Rango intercuartílico (IQR): determina las dimensiones de la caja o box en el gráfico. El IQR se calcula como la diferencia entre el percentil 25 (primer cuartil o \(Q_1\)) y el percentil 75 (tercer cuartil o \(Q_3\)) de la distribución de valores.
    • Valores dentro del “cuerpo principal” de la distribución: los “bigotes” o líneas a ambos lados de la caja se extienden en cada sentido hasta \(Q_1 - 1.5*IQR\) y \(Q_3 + 1.5*IQR\). Los valores que caen más allá de estos dos puntos a cada lado de la distribución se pueden considerar como valores atípicos (en inglés outliers).
    • Valores atípicos: se representan como puntos o símbolos individuales en el gráfico, a ambos lados del cuerpo principal de la distribución (si es que existen).
Figura 3.3: Explicación anotada de los elementos que componen un boxplot. Fuente: https://www.data-to-viz.com/caveat/boxplot.html.
  • Violín: Una importante limitación del boxplot es que al resumir el aspecto de la distribución de valores mediante un gráfico esquemático en forma de caja perdemos información sobre la forma de la distribución real de valores subyancente (la f.d.p.). En consecuencia, se han propuesto alternativas como, por ejemplo, el gráfico de violín (en inglés violing plot), que representa la estimación de la f.d.p. en ambos laterales de lo que sería la caja del boxplot, añadiendo más información al gráfico. Sin embargo, esta alternativa es, de igual modo, más difícil de interpretar.
Añadir jitter o puntos con desplazamiento aleatorio

Otra alternativa (quizá aún más confusa, depende de la situación) para añadir más información sobre la distribución de valores subyacente en el boxplot consiste en representar los elementos reales como puntos o símbolos superpuestos a la caja, como se representa en la Figura 3.4. Para poder ver todos los puntos se añade horizontalmente un pequeño desplazamiento aleatorio o jitter, de forma que se repartan por todo el área de la caja pero respetando su ubicación en la distribución de valores.

Figura 3.4: Cómo añadir puntos con jitter sobrepuestos al boxplot original. Fuente: https://r-graph-gallery.com/89-box-and-scatter-plot-with-ggplot2.html.

  • Strip charts: semejantes a los gráficos de boxplot con puntos sobrepuestos utilizando jitter, pero eliminando la representació esquemática de la caja y las líneas del cuerpo principal de la distribución. En ocasiones, la forma del gráfico de violín se combina con el strip chart para crear un swarm plot o beeswarm plot, que también se puede crear fácilmente en R con el paquete []ggbeeswarm](https://r-charts.com/distribution/ggbeeswarm/).

  • Histogramas apilados: se pueden apilar las barras de los histogramas para comparar diferentes distribuciones, aunque el gráfico resultante no es sencillo de interpretar para las distribuciones que no quedan en la parte inferior del gráfico (sólo se muestran con claridad diferencias acusadas entre grupos para el mismo intervalo).

  • Diagramas de densidad solapados: una ventaja de los diagramas de densidad de probabilidad es que permiten representar varios de ellos en el mismo gráfico sobrepuestos unos a otros, siempre que utilicemos transparencia en el color de relleno del área bajo cada curva o bien que sólo coloreemos las líneas de la distribución correspondiente a cada grupo. Un ejemplo se muestra en la Figura 3.5.

library(ggplot2)
library(dplyr)
library(tidyr)
library(viridisLite)

ggplot(data=diamonds, aes(x=price, group=cut, fill=cut)) +
    geom_density(adjust=1.5, alpha=.4)
Figura 3.5: Diagramas de densidad de probabilidad solapados para comparar las distribuciones correspondientes a varios grupos. Fuente: https://r-graph-gallery.com/135-stacked-density-graph.html.
  • Ridgeline plot: es una variante más organizada de los gráficos de densidad de probabilidad solapados. En este tipo de gráfico, se garantiza que todas las f.d.p. estimadas tienen la misma escala de representación horizontal, los mismos parámetros de configuración para el KDE y los gráficos para cada grupo se separan lo justo para permitir una comparación rápida y más precisa de las diferentes funciones de densidad estimadas.
library(ggridges)
library(ggplot2)
 
# Ejemplo básico de *ridgeplot*
ggplot(diamonds, aes(x = price, y = cut, fill = cut)) +
  geom_density_ridges() +
  theme_ridges()
Picking joint bandwidth of 458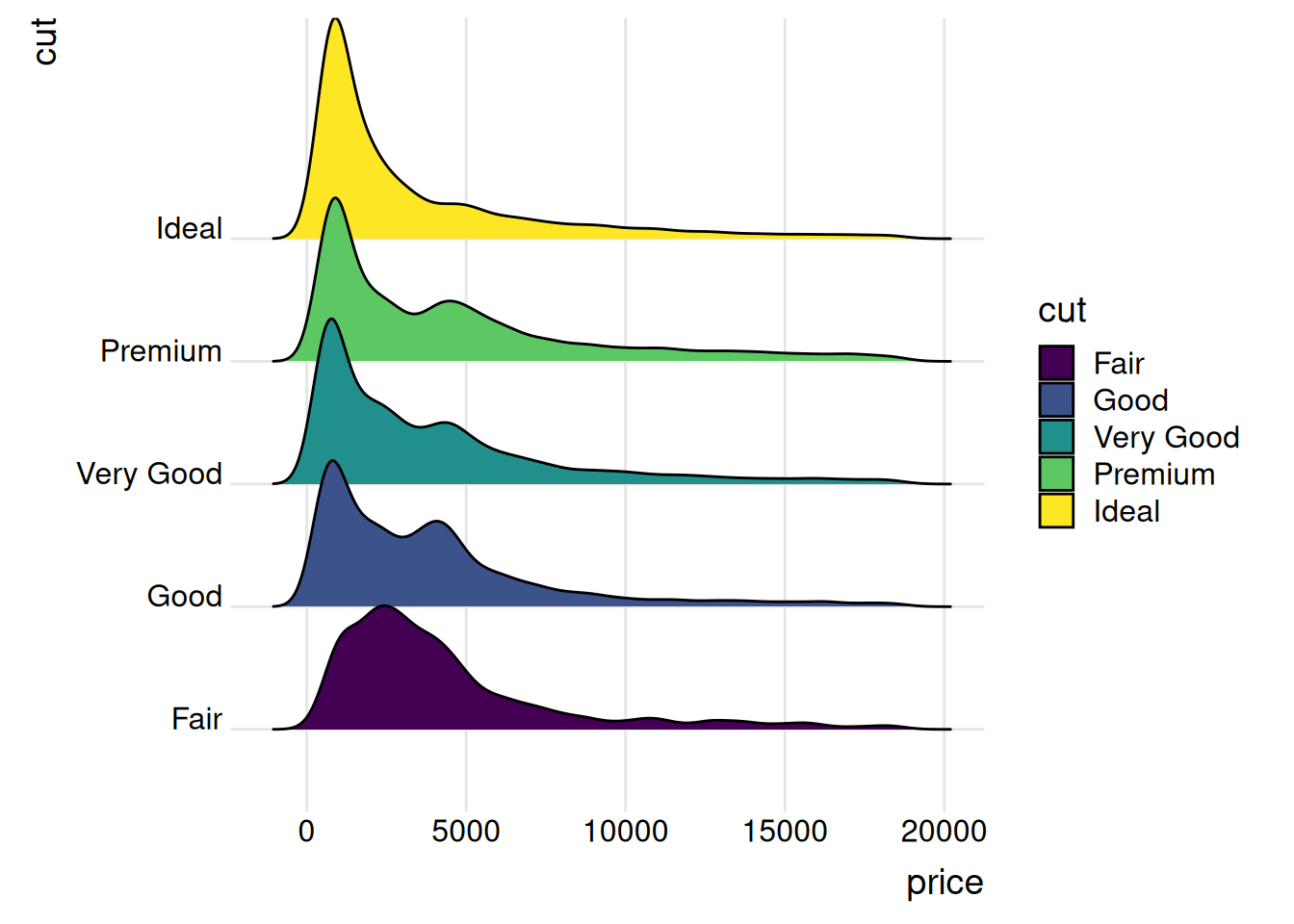
Figura 3.6: Ejemplo de un gráfido ridgeline creado mediante el paquete ggridges, extensión de ggplot2.

3.1.2 Relaciones cuantiativo-cuantitativo (gráficos X-Y)

En esta sección resumimos algunos gráficos para representación de relaciones entre variables cuantitativas en ambos ejes (suponiendo un gráfico 2D). Empezamos por los tipos báiscos que se muestran en la Figura 3.7.

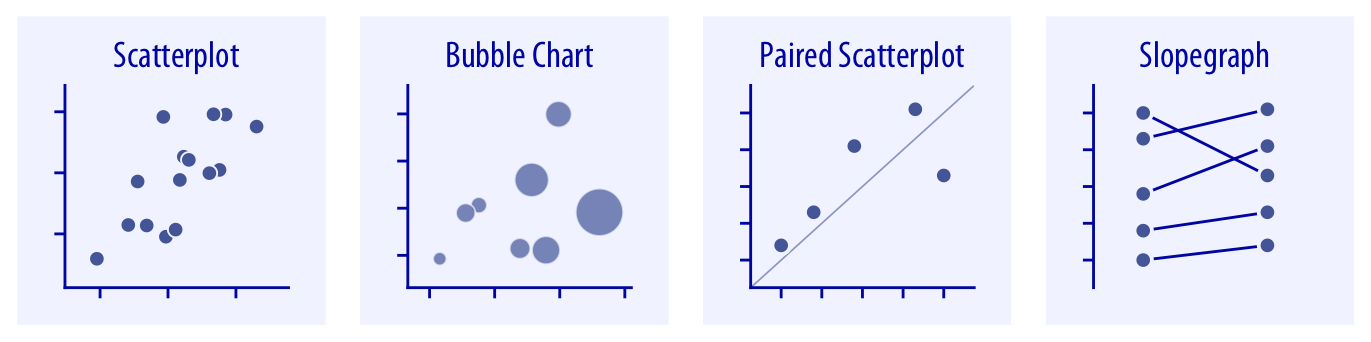
Figura 3.7: Algunos gráficos para representar relaciones entre valores de dos atributos numéricos. Fuente: (Wilke, 2019).

  • Gráfico de dispersión o scatterplot: es el típico gráfico de coordenadas cartesianas, representando cada elemento por un punto o un símbolo. En el caso de que, además, se quieran representar puntos pertenecientes a varias categorías se puede emplear un canal adicional (color, símbolo) con una leyenda para facilitar la interpretación del gráfico.

  • Gráfico de burbujas: permite representar simultáneamente tres atributos cuantitativos, utilizando el tamaño del círculo o burbuja para representar la tercera dimensión de los atributos.

  • Scatterplot emparejado: es un caso especial en el que se comparan dos medidas del mismo atributo o de atributos diferentes pero medidos en las mismas unidades y con la misma escala. En ese caso, suele ser útil representar la línea \(x=y\). Un ejemplo de este tipo de gráficos que hemos mencionado antes es el qqplot.

  • Slopegraph: otro tipo de gráfico para representar parejas de datos. Cada pareja de puntos se une mediante una línea horizontal, que nos da una idea de la variación que se ha producido entre los valores de esa pareja.

Continuamos con otro conjunto de gráficos que permiten resumir los datos usando curvas de nivel o contorno, intervalos o bins o correlogramas, que se muestran en la Figura 3.8.

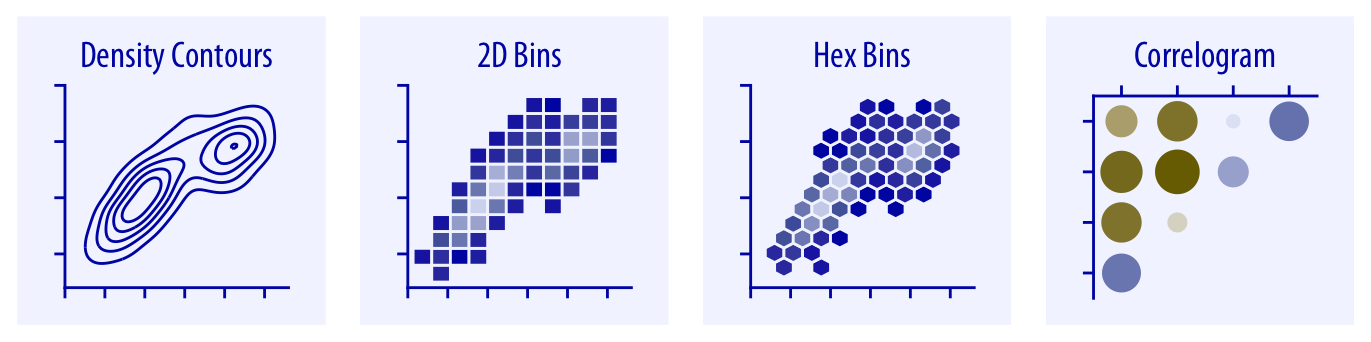
Figura 3.8: Algunos gráficos para resumir relaciones entre valores de dos atributos numéricos. Fuente: (Wilke, 2019).

  • Curvas de nivel: Las curvas de nivel permiten representar valores cuantitativos repartidos en una superficie continua, de forma que puedan ser interpretables.

  • Celdas o intervalos en 2D y hexagonales: Otra variante para representar datos cuantitativos repartidos en una superficie continua consiste en establecer primero una malla de celdas (cuadradas o hexagonales) representando mediante un canal (normalmente color) el valor promedio de la variable cuantitativa dentro de esa celda.

    • Una variante de los bins cuadrados en 2D es el gráfico de actividad que muestra número de acciones en cada periodo de tiempo (días, semanas, etc.). Un buen ejemplo son los gráficos de actividad para los perfiles de usuario de GitHub, como se muestra en la Figura 3.9.
Figura 3.9: Gráfico de actividad con bins en 2D que muestra el número de contribuciones diarias del usuario H. Wickham en GitHub. Fuente: https://github.com/hadley.
  • Correlograma: es un gráfico en el que se representa gráficamente el grado de correlación entre los valores de varios atributos. La representación concreta de cada correlograma puede variar mucho. Algunos utilizan el canal de color y una paleta divergente para distinguir claramente las correlaciones positivas o negativas. En otros casos se añaden más canales (cambios de forma, formas incompletas representando correlación parcial). La Figura 3.10 presenta un ejemplo de correlograma creado con el paquete ggcorrplot.
library(ggcorrplot)
library(colorspace)
data(mtcars)
corr <- round(cor(mtcars), 2)
my_palette <- diverging_hcl(3, palette = "Blue-Red")

ggcorrplot(corr, hc.order = TRUE, type = "lower",
   outline.col = "white",
   ggtheme = ggplot2::theme_gray,
   colors = my_palette)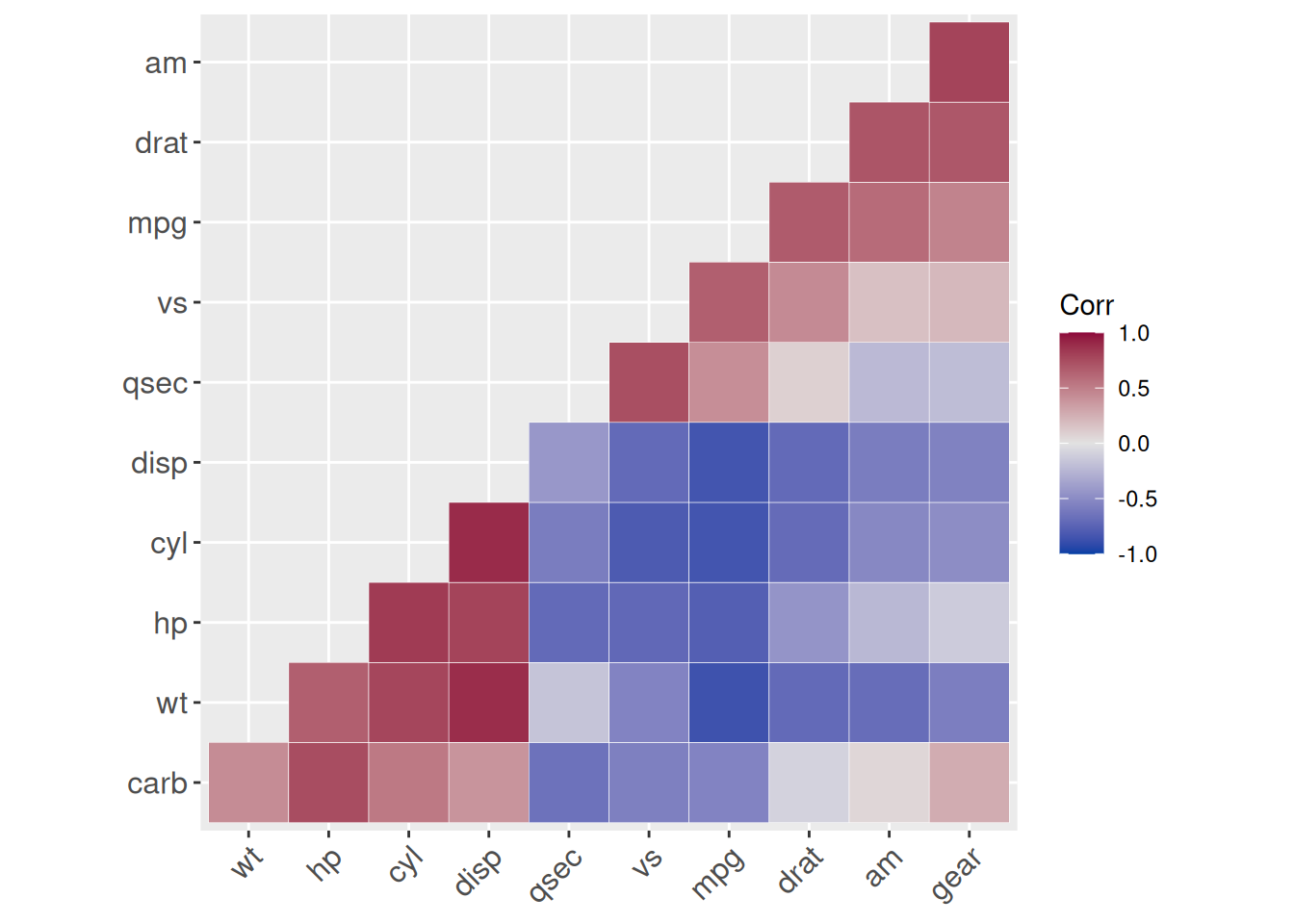
Figura 3.10: Correlograma para las variables cuantitativas del dataset mtcars producido con el paquete ggcorrplot.

Por último, existe un subconjunto de gráficos en esta categoría para representar datos con estricta dependencia temporal, o bien con dependencia de una variable con ordenación (por ejemplo, cantidad de dosis administrada de un fertilizante o un fungicida). También se encuentran en este subconjunto las líneas de estimación de tendencia o smooth line. Todos ellos se muestran en la Figura 3.11.

Figura 3.11: Algunos gráficos para representar valores numéricos con dependencia temporal, relacionados con variables ordenadas o para estimar tendencias. Fuente: (Wilke, 2019)
  • Gráfico de línea: los puntos o símbolos del gráfico se enlazan mediante una línea que remarca la secuencialidad entre las muestras. Un ejemplo de este tipo son los gráficos de series temporales, como el que se muestra en la
Figura 3.12: Series temporales del número total de envíos mensuales de artículos de investigación a tres servidores de preprints en investigación biomédica. Fuente: (Wilke, 2019); fuente de datos: Jordan Anaya, http://www.prepubmed.org/.

  • Scatterplot conectado: es un gráfico en el que se representan valores de un diagrama de dispersión conectados por lineas que denotan una secuencialidad temporal entre los elementos. Hay que usarlos con cuidado, sobre todo al construirlos, para que el resultado no sea difícil de intrepretar.

  • Línea suavizada de tendencia (smooth line): se trata de funciones suavizadas que resumen tendencias globales de los valores en gráficos de dispersión. Existen diversos algoritmos para generarlas, como por ejemplo el LOESS (Cleveland et al., 1992) o LOWESS (Cleveland, 1981). Veamos un ejemplo con el paquete ggplot2 y la función integrada geom_smooth(), ilustrado en la Figura 3.13.

ggplot(mpg, aes(displ, hwy)) + 
  geom_point() +
  geom_smooth(method = "loess", formula = 'y ~ x') + 
  facet_wrap(~year)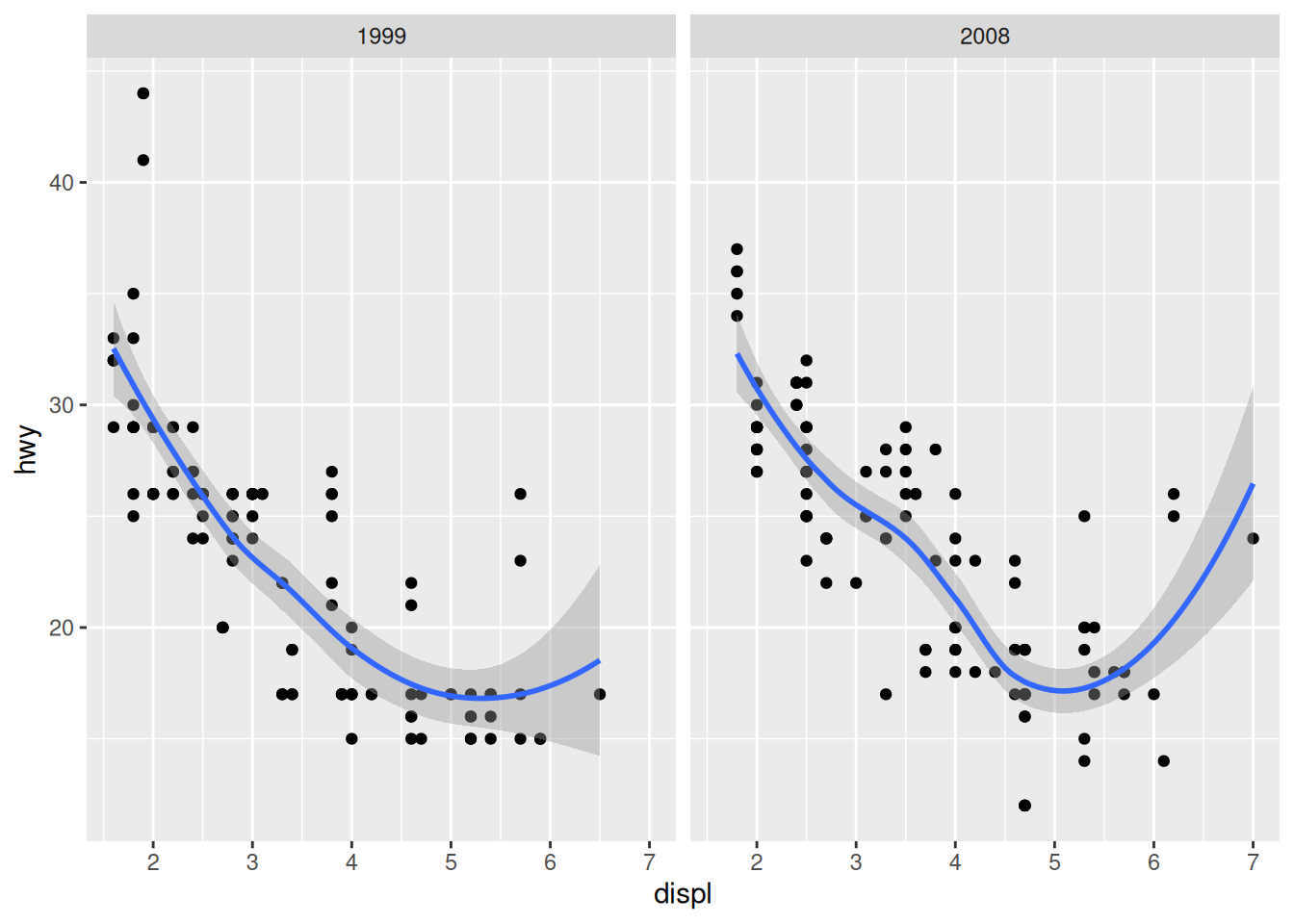
Figura 3.13: Diagramas de dispersión comparando el cubicaje y la autonomía de diferentes modelos de automóviles en 1999 y 2008.

3.1.3 Relaciones cuantitativo-cualitativo

En la Figura 3.14 se muestran los tipos básicos de gráficos para representación de valores numéricos frente a valores de una variable categórica.

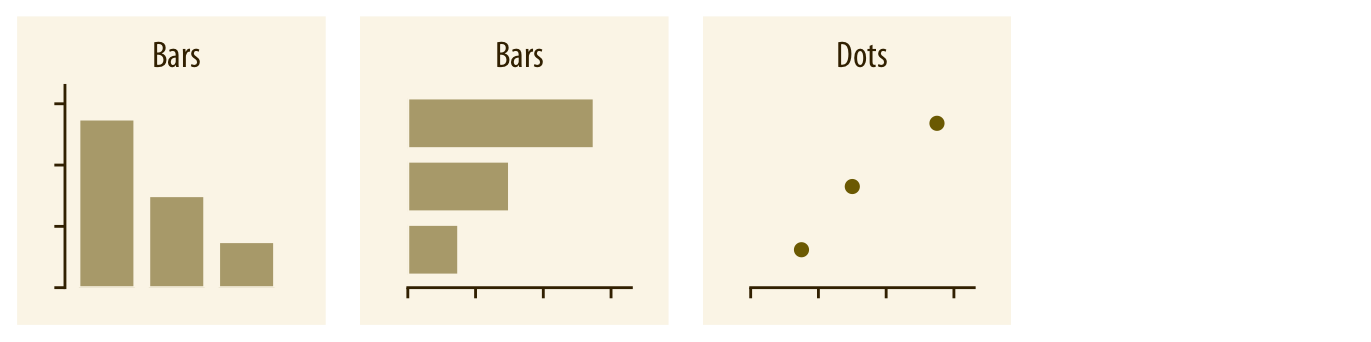
Figura 3.14: Gráficos para representar relaciones entre un atributo cuantitativo y otro categórico. Fuente: (Wilke, 2019).

  • Diagrama de barras: este tipo de gráfico es sobradamente conocido. Permite representar cifras correspondientes a varias categorías para compararlas entre sí. No obstante, hay algunos aspectos que pueden facilitar su interpretación:

    • Barras horizontales: cambiar la orientación de las barras puede ser una buena estrategia si estamos comparando muchas categorías y las diferencias entre ellas no son muy grandes. Esto se debe a que nuestra percepción visual de las diferencias entre objetos horizontales es más precisa que cuando los objetos se orientan verticalmente.

    • Ordenación de las barras: podemos ordenar las barras en sentido creciente o decreciente para ayudar a nuestra audiencia a identificar rápidamente los casos extremos, siempre y cuando no estemos obligados a ordenar las categorías por algún otro criterio específico.

  • Dotplot (diagrama de puntos): propuesto por W. S. Cleveland (Cleveland, s. f.) para simplificar la representación de la información en un diagrama de barras. Es compatible con la representación de intervalos de confianza y barras de error. Además, permite también comparar resultados entre grupos para cada categoría, tal y como muestra la Figura 3.15, lo que aumenta aún más si cabe su utilidad.

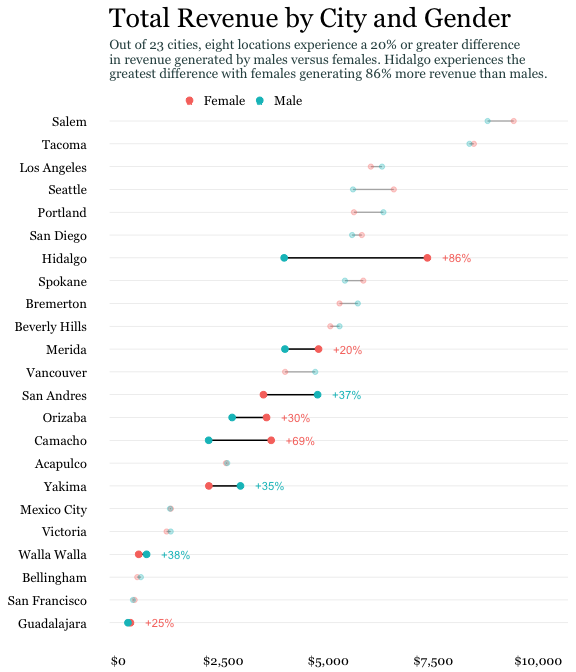
Figura 3.15: Ejemplo de un Cleveland dotplot que compara los ingresos de mujeres y hombres en varias ciudades de EE.UU. Fuente: https://uc-r.github.io/cleveland-dot-plots

En este ejemplo, podemos observar que las ciudades se han ordenado de mayor a menor cantidad de ingresos. También se ha utilizado el canal color para distinguir los puntos correspondientes a los ingresos de los hombres respecto a los de las mujeres y se ha añadido una anotación que cuantifica su diferencia positiva o negativa. El subtítulo del gráfico muestra algunas conclusiones principales, con lo que podemos interpretar el gráfico con mayor rapidez.

Confusión con el término dotplot

Aunque el término dotplot fue propuesto inicialmente por W. S. Cleveland en 1984 y tiene un claro significado para gran parte de la comunidad de visualización de datos (remarcado, en ocasiones, anteponiendo el apellido de su creador), herramientas actuales como ggplot2 incluyen una función geom_dotplot() que no tiene nada que ver con este tipo de gráfico, como podemos comprobar en los ejemplos de la documentación oficial.

Esta desafortunada ambigüedad no se va a poder corregir fácilmente, puesto que la API de ggplot2 ya está muy consolidada. Para agravar aún más si cabe esta confusión, podemos encontrar el tipo de gráfico dotplot original de Cleveland bajo otros seudónimos, como lollipop plot.

Como siempre, lo importante es entender bien el concepto y el tipo de gráfico que queremos construir.

La Figura 3.16 muestra gráficos para representar relaciones entre una variable cuantitativa y varias categorías de manera simultánea en la misma imagen.

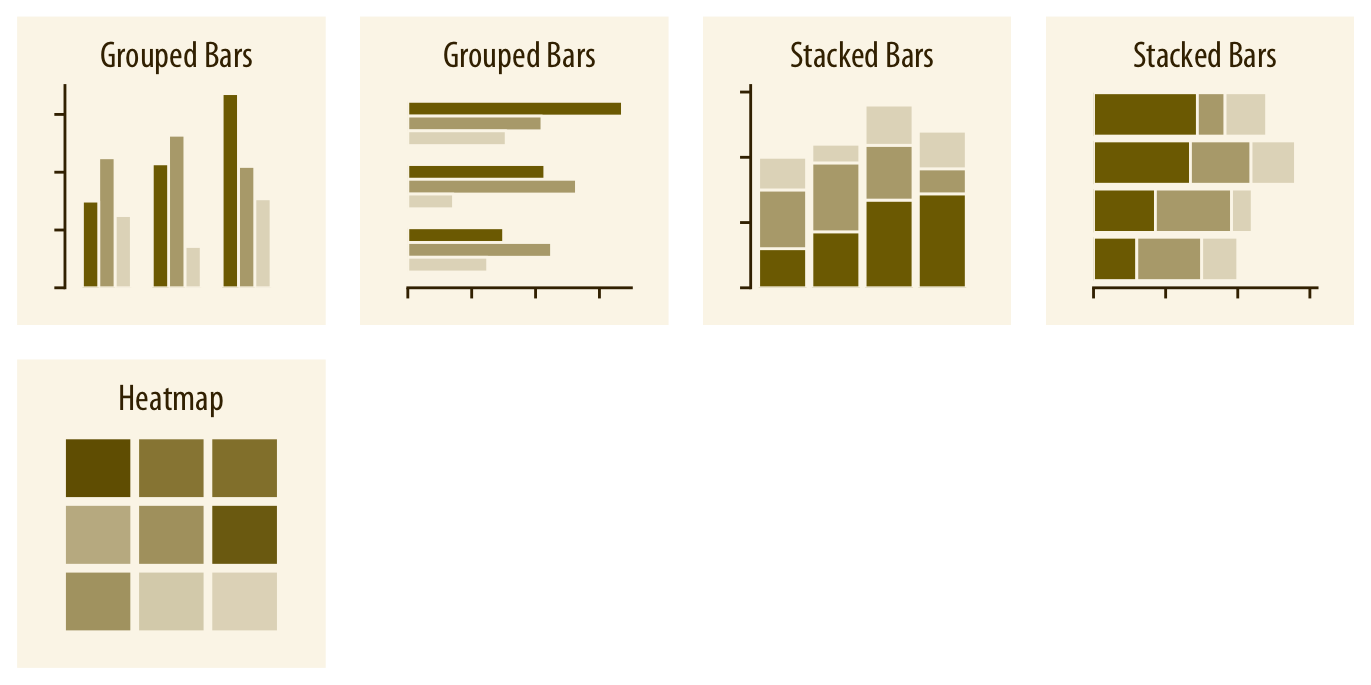
Figura 3.16: Gráficos para representar relaciones entre un atributo cuantitativo y varias categorías simultáneamente. Fuente: (Wilke, 2019).

  • Diagrama de barras agrupado: como el diagrama de barras tradicional, pero añadiendo dentro de cada categoría principal una barra por cada categoría de la segunda variable cualitativa que estamos comparando. Para evitar repetir la etiqueta de los valores de la segunda categoría en cada grupo, normalmente se usa otro canal (color) para distinguirlas, indicando en una leyenda en nombre de la categoría de la segunda variable que corresponde a cada valor del canal.

  • Diagrama de barras apiladas (stacked bars): cuando el objetivo es comparar los valores de una subcategoría con los de esa misma subcategoría en otras categorías principales del gráfico, podemos crear un diagrama de barras apilado para comprar más directamente los segmentos de cada subcategoría.

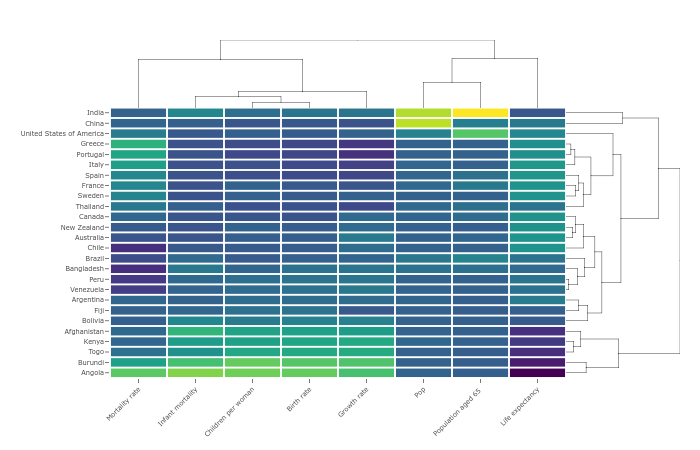
  • Mapa de calor (heatmap): permite comparar diferentes ítems según los valores de una variable cuantitativa obtenidos para dos variables categóricas simultáneamente. En R se pueden construir un heatmap utilizando varios paquetes, obteniendo tanto gráficos estáticos como interactivos (dinámicos). Un ejemplo se muestra en la Figura 3.17, con una captura estática de un heatmap interactivo para comparar varios países en función de los valores obtenidos en varios índices de medición de nivel de bienestar y desarrollo en cada país. Este heatmap también incorpora un dendongrama en cada margen, ofreciendo pistas adicionales sobre los países más similares entre sí (consulta la referencia para ver el código fuente que genera este gráfico).

Figura 3.17: Mapa de calor (heatmap) para comparar varios países según los valores de diferentes índices de bienestar y desarrollo en cada uno de ellos. Fuente: https://www.data-to-viz.com/graph/heatmap.html.

3.1.4 Proporciones

Los gráficos básicos para representación de proporciones están resumidos en la Figura 3.18.

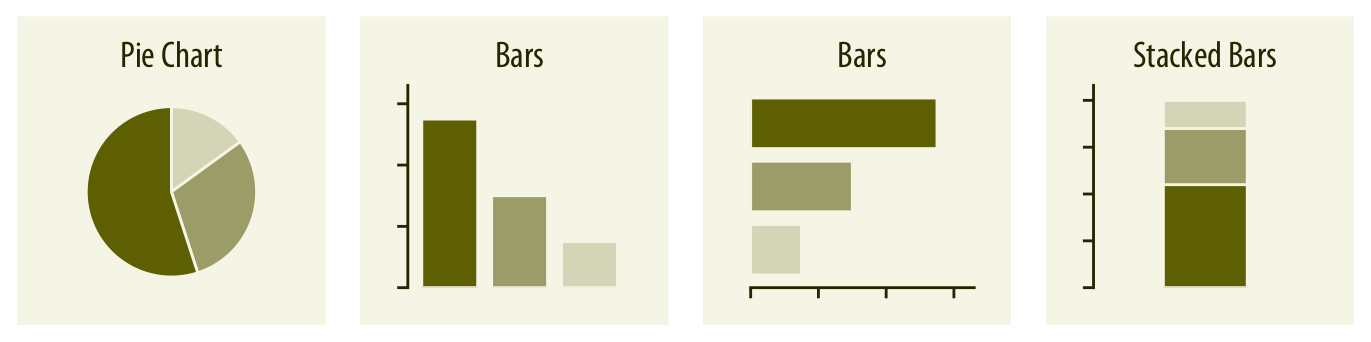
Figura 3.18: Gráficos básicos para representación de proporciones. Fuente: (Wilke, 2019).

  • Diagrama de sectores (pie chart): otro tipo de gráfico sobradamente conocido y, dicho sea también, muy denostado en la comunidad de visualización de datos por sus dudosas propiedades para reflejar de forma precisa la información que queremos comparar, sobre todo si las categorías tienen porcentajes muy semejantes (es decir, si los sectores tienen tamaños muy parecidos).

  • Diagrama de barras (porcentual): en este caso cada barra refleja proporciones (en %) y no valores absolutos de un atributo numérico.

A su vez, la Figura 3.19 muestra distintos tipos de diagramas para representar mútiples conjuntos de proporciones.

Figura 3.19: Gráficos básicos para representación de múltiples conjuntos de proporciones. Fuente: (Wilke, 2019).

  • Diagramas de sectores múltiples: cuidado con este tipo de gráfico, puesto que si ya es complicado en ocasiones comparar los sectores en un solo diagrama imaginemos cómo se complica la tarea cuando hay que comparar sectores de varios diagramas de forma simultánea.

  • Diagramas de barras agrupados y apilados: son aplicables los mismos comentarios que en el caso de representación de valores absolutos. No obstante, en el caso de las proporciones suele ser más preciso y útil para interpretar el gráfico usar la modalidad de barras apiladas.

  • Diagramas de densidades apiladas: ofrecen una solución rápida para comparar proporciones. Sin embargo, tiene dos desventajas. La primera es que usamos demasiada “tinta” para el gráfico. La segunda es que es complicado interpretar la distribución de valores para cualquier categoría excepto la que está en la base del gráfico. Podemos ver un ejemplo de este tipo de gráficos para comprender mejor sus ventajas e inconvenientes.

Por último, la Figura 3.20 muestra gráficos para desglosar proporciones en función de más de una variable categórica a la vez en la misma figura.

Figura 3.20: Gráficos para representación de proporciones en función de más de una categoría de forma simultánea. Fuente: (Wilke, 2019).
  • Gráfico de mosaico (mosaic plot): permite crear áreas coloreadas para comparar proporciones entre dos o más atributos categóricos a la vez. Si comparamos más de dos variables cualitativas, tendremos que hacer un mosaic plot para cada categoría de la tercera variable. En la Figura 3.21 se presenta un ejemplo de gráfico de mosaico para comparar los porcentajes de respuestas a dos preguntas de un cuestionario.
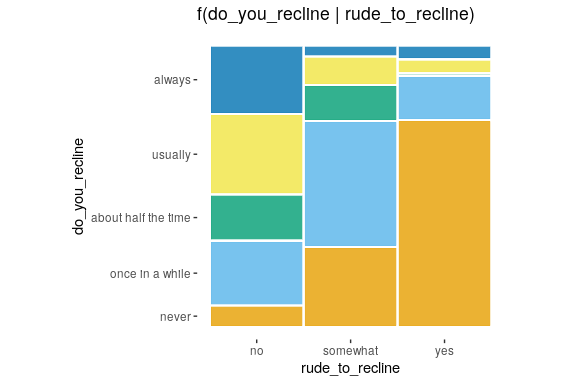
Figura 3.21: Ejemplo de un gráfico de mosaico creado con el paquete ggmosaic en R. Fuente: <https://cran.r-project.org/web/packages/ggmosaic/vignettes/ggmosaic.html
  • Treemap: a pesar de su parecido con los gráficos de mosaico, el treemap tiene una diferencia importante, que radica en que representamos datos jerárquicos como un conjunto de rectángulos anidados. Por tanto, sólo es válido para representar proporciones de subcategorías que se unen para formar otra categoría mayor, como vemos en el ejemplo de la Figura 3.22.
Figura 3.22: Ejemplo de un treemap que representa proporciones de varias subcategorías dentro de tres categorías principales. Fuente: https://r-graph-gallery.com/235-treemap-with-subgroups.html.
  • Conjuntos paralelos (parallel sets o alluvial plot): se trata de un gráfico algo más difícil de intrepretar a primera vista, pero de enorme utilidad cuando conseguimos entender su mecánica funcional. Representa el porcentaje de una categoría que va a parar al resto de categorías de otra u otras variables (se pueden añadir más variables a la derecha, pero cada vez es más complicado “seguirle al pista” a los flujos). La Figura 3.23 presenta un ejemplo de este tipo de gráficos, mostrando el desglose de pasajeros del viaje inaugural del Titanic en función de diversos factores: cubierta donde se alojaban, género y rango de edad. El paquete ggalluvial facilita la construcción de este tipo de gráficos en R con ggplot2 (Brunson, 2020).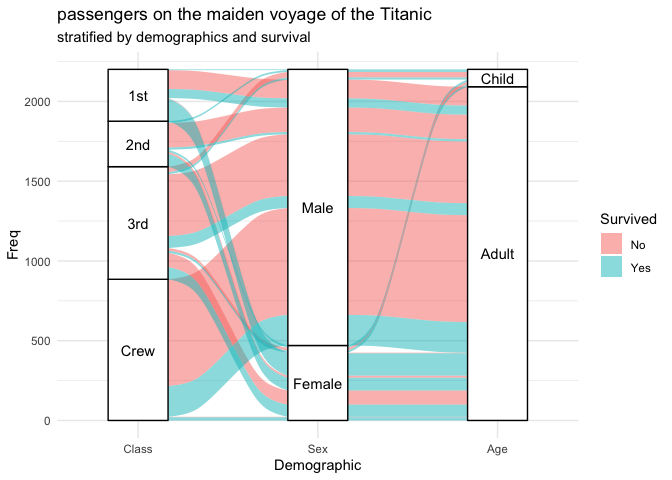
Figura 3.23: Ejemplo de un alluvial plot para desglosar los pasajeros del viaje inaugural del Titanic según tres posibles factores. Fuente: https://corybrunson.github.io/ggalluvial/

3.1.5 Datos espaciales

La Figura 3.24 muestra algunos gráficos básicos para representación de datos con dependencias espaciales.

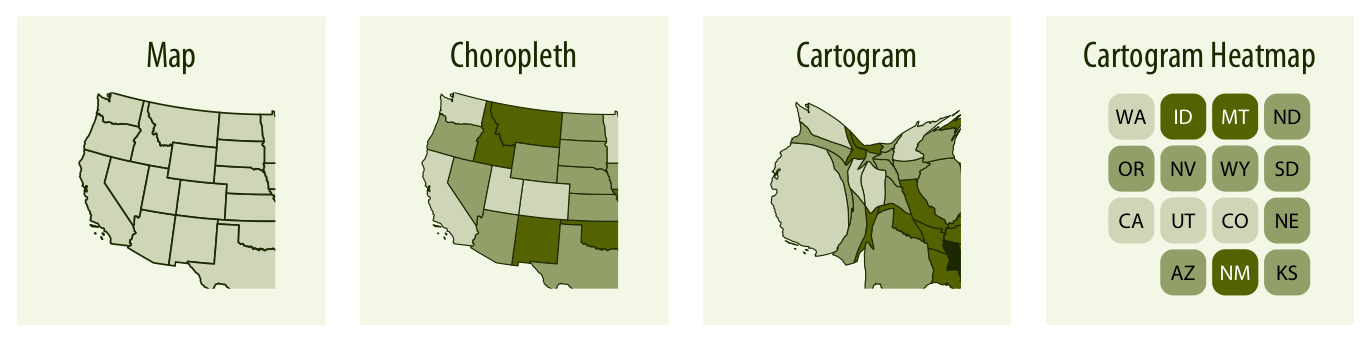
Figura 3.24: Gráficos básicos para representación de datos espaciales. Fuente: (Wilke, 2019).

  • Mapa: como resulta evidente, la opción más directa es representar datos geolocalizados mediante algún tipo de mapa (político, geográfico, etc.), posiblemente enriquecido con información adicional para proporcionar más contexto. En el Capítulo 8 veremos más detalles, aunque este tipo de gráficos no son el objeto principal de este taller, debido a que requieren gran cantidad de conceptos y herramientas propias de este dominio. Para más información, se recomienda consultar referencias actualizadas y de calidad como https://r.geocompx.org/ (Lovelace et al., 2025) o https://r-spatial.org/book/ (Pebesma & Bivand, 2023).

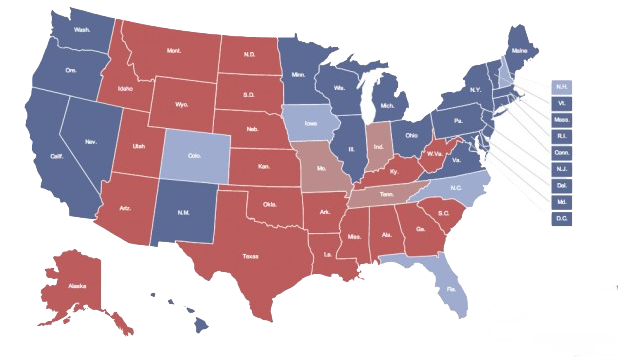
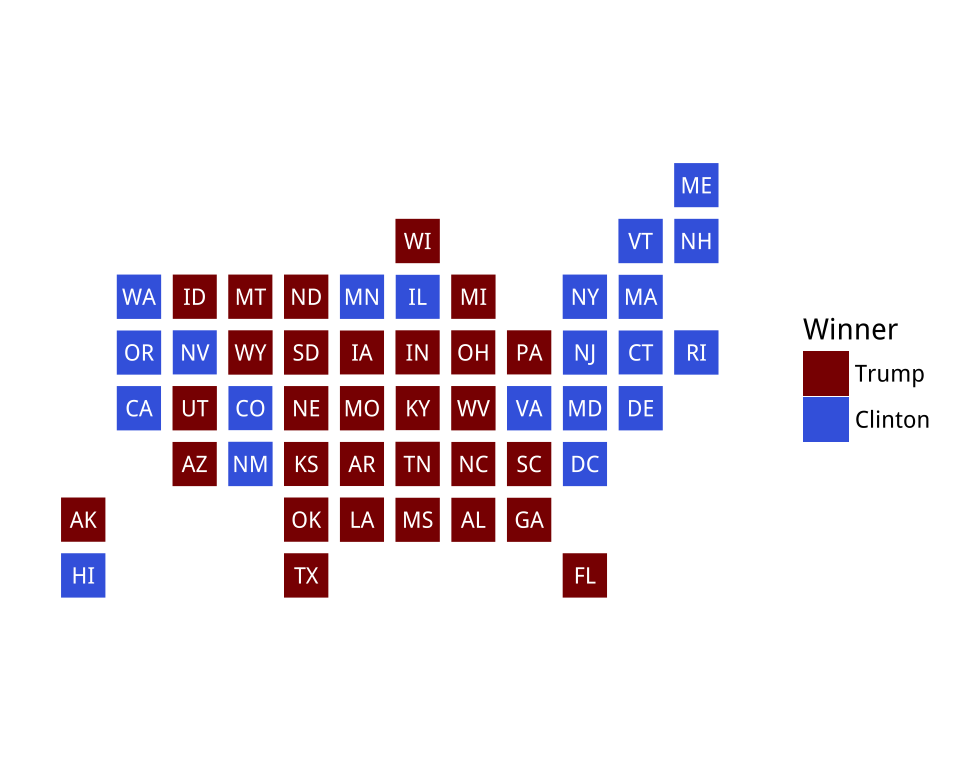
  • Choropleth: es un tipo de mapa en el que se colorean, sombrean o degradan las regiones según los valores de cierto atributo. Tienen un gran poder explicativo, especialmente cuando las unidades espaciales nos resultan familiares, como una región o el mápa político de un país. Un ejemplo se muestra en la Figura 3.25

Figura 3.25: Choropleth que representa los resultados de las elecciones presidenciales en EE.UU. de 2016. Fuente: https://socviz.co/maps.html.
  • Cartograma y artograma de calor (cartogram heatmap): Son gráficos en los que se muestra esquemáticamente los resultados de variables geolocalizadas, sin utilizar los polígonos correspondientes a las regiones reales. Un ejemplo de este tipo de gráficos se muestra en la Figura 3.26.
Figura 3.26: Cartograma que representa esquemáticamente los resultados de las elecciones presidenciaels en EE.UU. de 2016. Fuente: https://socviz.co/maps.html

3.1.6 Representación de la incertidumbre

La Figura 3.27 muestra varios ejemplos de gráficos que representan márgenes de error en medidas o estimaciones estadísticas.

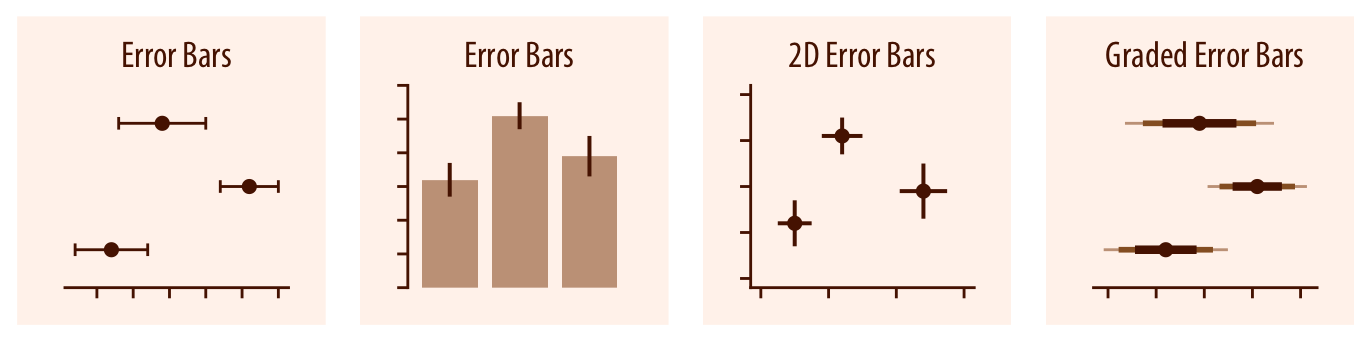
Figura 3.27: Gráficos básicos para representación de barras de estimaciones de error. Fuente: (Wilke, 2019).

  • Barras de error: cuando los diagramas de barras representan valores estadísticos, como media, mediana, desviación típica, etc. es aconsejable añadir barras de error sobre la parte superior de cada barra, para indicar la variabilidad en la estimación. Un ejemplo de esta práctica se ilustra en la Figura 3.28.

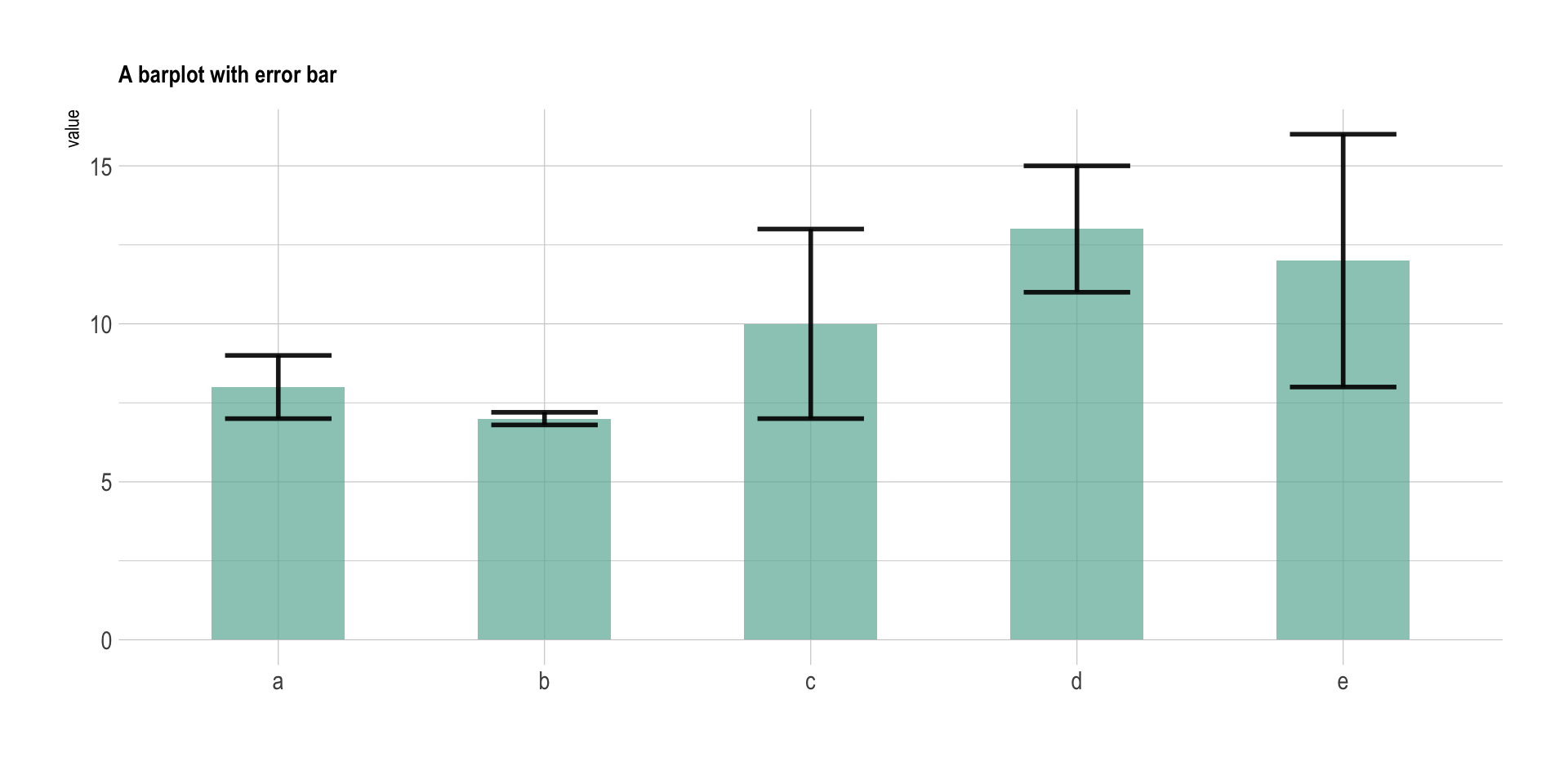
    Figura 3.28: Ejemplo de un gráfico de barras que incluye barras de error. Fuente: https://www.data-to-viz.com/caveat/error_bar.html.

    Sin embargo, la utilización de barras de error puede ocultar información valiosa al espectador, como se muestra en la Figura 3.29. Vemos que el mismo diagrama de barras con barras de error corresponde con diferentes distribuciones de los datos. Por ese motivo, se desaconseja en muchos casos usar este tipo de diagramas, en favor de la utilización del boxplot, violin plot, swarm plot o alguna otra variante que muestre información adicional sobre la distribución de los datos originales.

    Figura 3.29: Ejemplo de un gráfico de barras que incluye barras de error y corresponde a diferentes distribuciones de datos subyacentes. Fuente: https://www.data-to-viz.com/caveat/error_bar.html.

A su vez, la Figura 3.30 muestra varios ejemplos de gráficos para visualización de la distribución de probabilidad en intervalos de confianza o en modelos (a priori y a posteriori).

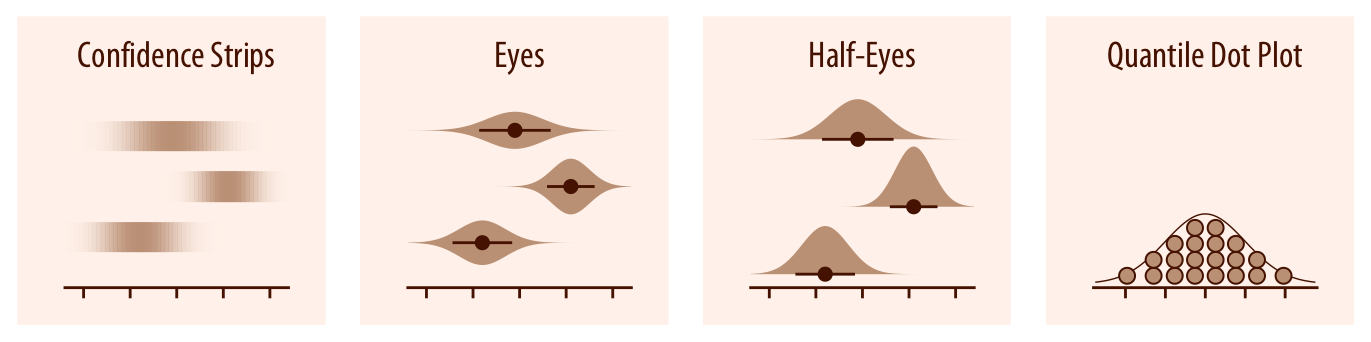
Figura 3.30: Gráficos básicos para representación de estimaciones estadísticas. Fuente: (Wilke, 2019).

En este caso, conviene destacar que lo más importante es dejar claro a nuestra audiencia qué representan las bandas o intervalos de confianza, de forma que los resultados se puedan interpretar sin cometer errores.

Por último, tenemos algunas modalidades para representar bandas de intervalos de confianza en estimaciones gráficas (curvas resultado de ajustes y modelos), que suelen incluir diferentes anchos o gradaciones para indicar diferentes intervalos en el mismo gráfico (c.i. 90%; c.i. 95%, etc.). Varios ejemplos aparecen esquematizados en la Figura 3.31.

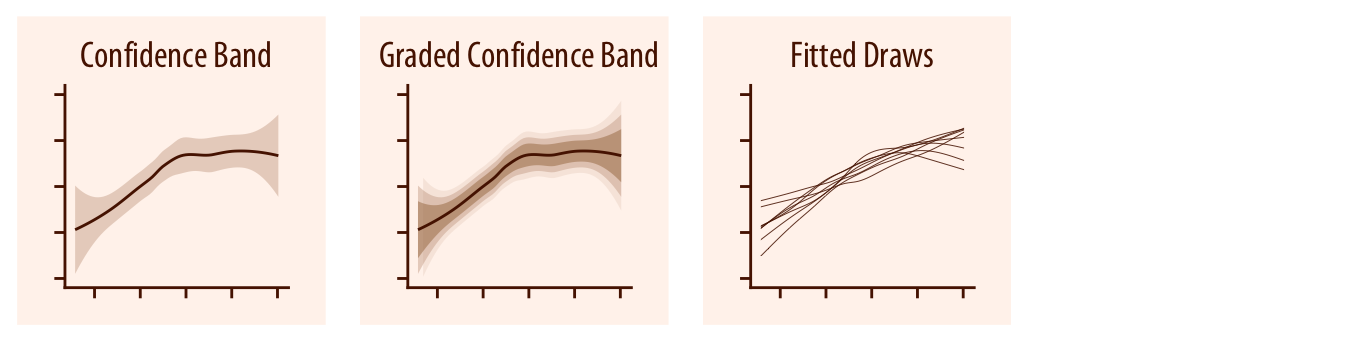
Figura 3.31: Gráficos básicos para representación de intervalos de confianza en estimaciones. Fuente: (Wilke, 2019).

El caso más habitual es el de mostrar bandas a amobs lados de una recta o curva estimada a partir de un modelo estadístico ajustado a nuestros datos. El gráfico de la Figura 3.32 muestra cómo se puede implementar con el paquete ggplot2.

library(ggplot2)

# Creamos el gráfico de dispersión y añadimos bandas en azul claro
# marcando el intervalo de confianza al 95% (opción por defecto)
ggplot(data=mtcars, aes(x=mpg, y=wt)) +
  geom_point() +
  geom_smooth(method=lm, color='red', fill='lightblue')
`geom_smooth()` using formula = 'y ~ x'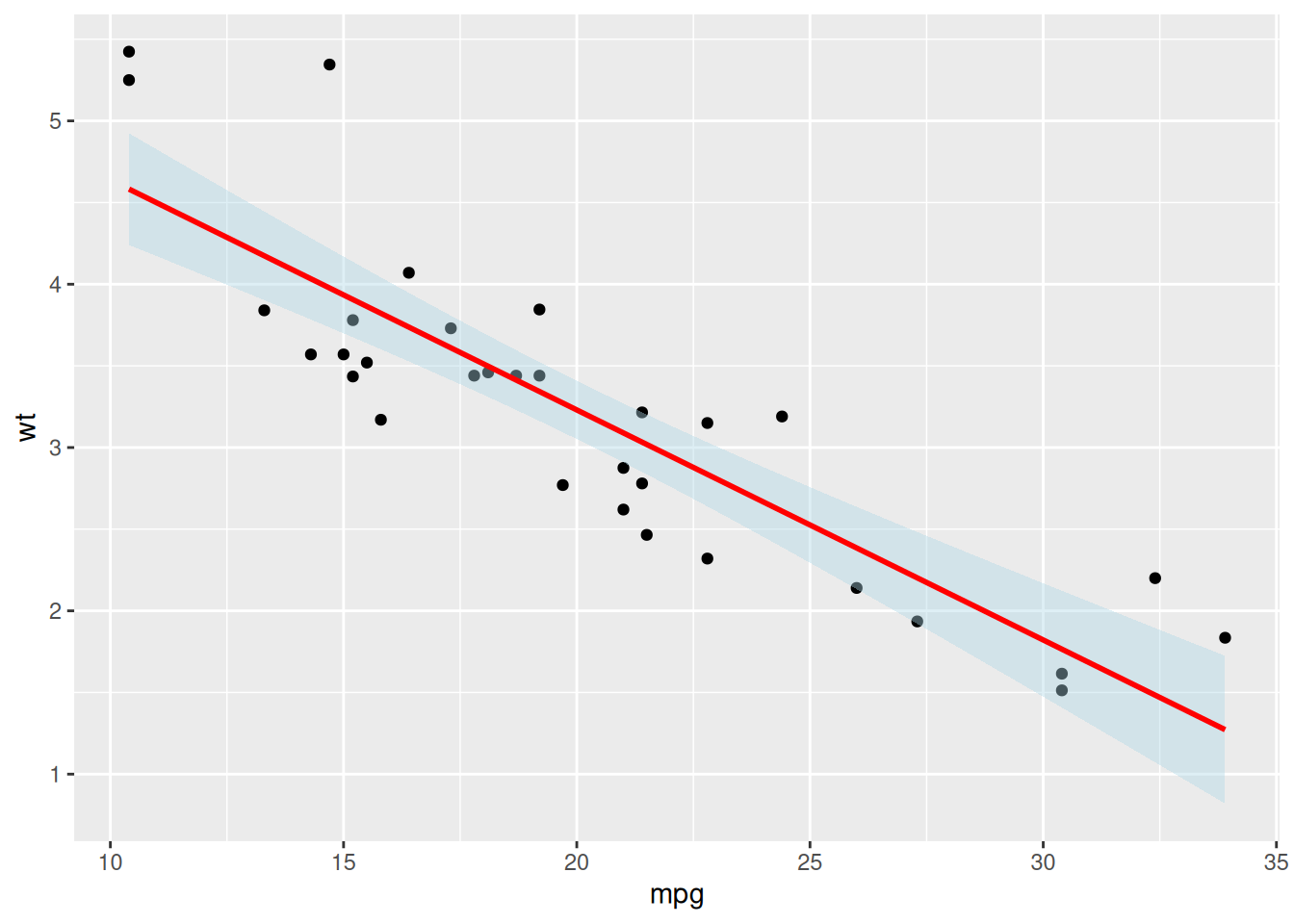
Figura 3.32: Ilustración de un intervalo de confianza del 95% alrededor de una recta de regresión simple ajustada a una nube de puntos

3.2 Árbol de decisión: ¿qué grafico escojo?

Como conclusión de este capítulo, seguramente podremos pensar que el gran número de tipos de gráficos de entre los que podemos escoger para nuestro propio trabajo es abrumador. Afortunadamente, existen algunas guías que permiten plantearnos unas sencillas preguntas de diseño para orientar nuestra elección, reduciendo al menos el alcance de la búsqueda a un subconjunto de tipos de gráficos que mejor se adapte a nuestro problema particular.

El sito web https://www.data-to-viz.com/ publica una imagen en alta resolución (que se puede recibir por correo-e), en la que se resume un sencillo diagrama de decisión para orientar nuestra selección del gráfico más apropiado. En todo caso, esperamos que los comentarios y orientaciones que hemos incluido en este capítulo permitan a futuros creadores/as de gráficos seleccionar con criterios las herramientas a emplear.